표본의 크기 결정 (평균추정을 위한, 비율 추정을 위한)

오늘은 통계학의 세계에서 정말 중요한 주제인 ‘표본 크기 결정’에 대해서 이야기해보려고 합니다.

많은 분들이 연구나 조사를 계획할 때 “과연 몇 명을 대상으로 설문조사를 해야 할까?”라는 질문에 봉착하곤 하죠. 이 때 필요한 것이 바로 표본 크기 결정이에요!

안녕하세요, 여러분! 오늘은 통계학의 세계에서 정말 중요한 주제인 ‘표본 크기 결정’에 대해서 이야기해보려고 합니다. 많은 분들이 연구나 조사를 계획할 때 “과연 몇 명을 대상으로 설문조사를 해야 할까?”라는 질문에 봉착하곤 하죠. 이 때 필요한 것이 바로 표본 크기 결정이에요!

• 조사하고자하는 변수의 분산값이 클수록 표본의 크기는 커야함
• 추정치에 대한 높은 신뢰수준을 원할수록, 표본크기는 커져야 함
• 허용오차가 작을수록, 표본 크기는 커야함

1) 평균 추정을 위한 표본 크기 결정:

우선, 평균 값을 추정하고 싶을 때 표본 크기를 어떻게 결정해야 하는지 알아볼까요?

예를 들어, 우리가 알고 싶은 것이 어떤 지역의 주민들의 평균 소득일 수 있습니다. 이 경우, 우리가 필요로 하는 것은 바로 ‘정확한’ 추정치입니다.

이 때 중요한 요소는 세 가지입니다:

1. 조사하고자 하는 변수의 분산값: 이 값이 클수록, 우리가 필요로 하는 표본의 크기도 커집니다. 왜냐하면, 데이터가 넓게 퍼져 있을수록 더 많은 사람들을 조사해야 평균값에 대한 좋은 추정치를 얻을 수 있기 때문이죠.
2. 신뢰수준: 이것은 우리가 얼마나 ‘확신’을 갖고 싶어하는지와 관련이 있어요. 일반적으로 사용되는 신뢰수준은 95%인데, 이는 우리가 100번 조사를 실시할 때 95번은 우리의 추정치가 실제 평균값을 포함할 것이라는 뜻입니다. 신뢰수준을 높이면 높일수록, 당연히 더 많은 사람들을 조사해야 해요.
3. 허용오차: 이것은 우리가 어느 정도의 오차를 받아들일 준비가 되어 있는지를 나타냅니다. 허용오차를 줄이고 싶다면, 즉 더 정확한 추정치를 원한다면, 더 많은 사람들을 조사해야 하죠.

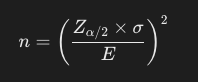
예를 들어, 95% 신뢰 수준에서 표준 편차가 10이고, 허용 오차를 2로 설정한다면, 필요한 표본 크기
n은 다음과 같이 계산됩니다:

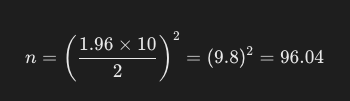
따라서, 약 96명의 표본 크기가 필요합니다. 이 공식을 사용할 때는 항상 결과값을 올림하여 실제 조사나 실험에 필요한 최소 표본 크기를 결정해야 합니다.

2) 비율 추정을 위한 표본 크기 결정:

이제, 비율을 추정하고자 할 때는 어떻게 해야 할까요? 예를 들어, 우리가 알고 싶은 것이 특정 정책에 대한 지지율일 수 있습니다.

비율 추정의 경우에도 비슷한 원리가 적용되요:

1. 분산값: 이 경우, 최대 분산을 가정하는 것이 일반적입니다(0.25라고 가정, 즉 p(1-p)의 최대값에서 p=0.5일 때). 왜냐하면, 우리는 특정 비율에 대한 사전 정보가 없을 때 이 가정을 사용하게 되기 때문입니다.
2. 신뢰수준과 허용오차: 이 두 가지 요소는 평균 추정과 마찬가지로 적용됩니다. 높은 신뢰수준과 낮은 허용오차를 원한다면, 더 많은 표본이 필요하죠.

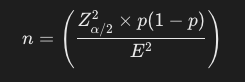
예를 들어, 95% 신뢰 수준에서 실제 비율에 대한 사전 정보가 없고, 허용 오차를 5%로 설정한다면, 필요한 표본 크기 n은 다음과 같이 계산됩니다.

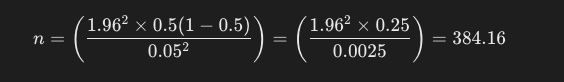
따라서, 약 385명의 표본 크기가 필요합니다 (결과값을 항상 올림). 이 공식을 사용하면, 설정한 신뢰 수준과 허용 오차 내에서 모집단 비율을 추정할 수 있는 표본의 크기를 결정할 수 있습니다.