단일 모집단 평균 차이 검증 (t-test) 이론, 공식, 검증절차

쉽게 이해하는 단일모집단 평균차이 검증(t) 이론

단일 모집단 평균 차이 검증, 즉 일표본 t-검정(One-Sample t-Test)은 통계학에서 사용하는 방법 중 하나로, 우리가 관심을 갖는 그룹(모집단)의 평균이 특정한 값(가설로 설정한 값)과 같은지 다른지를 알아보기 위해 사용합니다.

쉽게 말해, 일표본 t-검정은 마치 “우리 반의 평균 키가 160cm라고 할 수 있을까?”와 같은 질문을 수학적으로 검증하는 방법입니다.
여기서 ‘우리 반의 평균 키’는 검사하고자 하는 모집단의 평균이고, ‘160cm’는 우리가 검증하고 싶은 특정 값입니다.

검증 방법:

1. 가설 설정: 먼저, 두 가지 가설을 세웁니다.

• 귀무가설(H0): 우리 반의 평균 키는 160cm이다. (즉, 차이가 없다)
• 대립가설(H1): 우리 반의 평균 키는 160cm가 아니다. (즉, 차이가 있다)

1. 데이터 수집: 우리 반 학생들의 키 데이터를 모읍니다.
2. t-값 계산: 수집된 데이터를 바탕으로, 실제 평균과 가설로 설정한 평균(160cm)과의 차이를 t-값이라는 통계량으로 계산합니다. 이 때, 데이터의 분산과 학생 수도 계산에 포함됩니다.
3. 결과 해석: 계산된 t-값을 기준으로, 특정 확률(일반적으로 5% 또는 1%) 아래에서 이러한 차이가 우연히 발생할 확률(p-value)을 찾습니다.

• 만약 이 확률(p-value)이 매우 낮다면 (예를 들어, 0.05보다 작다면), 우리는 귀무가설을 기각하고 ‘우리 반의 평균 키는 160cm가 아니라고 결론 내립니다.
• 만약 이 확률이 높다면 (예를 들어, 0.05보다 크다면), 귀무가설을 기각할 충분한 증거가 없다고 보고, ‘우리 반의 평균 키가 160cm일 수 있다’고 결론 내립니다.

단순화시켜 말하자면, 일표본 t-검정은 우리가 가지고 있는 데이터가 우리의 가정(귀무가설)과 얼마나 잘 맞는지를 측정하는 방법입니다.

단일모집단 평균 차이 검증(t) 통계량 공식

자, 공식을 외우기란 쉽지 않습니다. 논리적으로 해석하여 이해해보도록 할게요.

1. 분자의 역할: ( \bar{x} – \mu_0 )

분자는 표본 평균과 귀무가설의 평균 간의 차이를 나타냅니다. 이 차이가 크면 클수록, 실제 표본 데이터와 귀무가설 간에 큰 차이가 있음을 의미합니다. 즉, 우리의 표본이 귀무가설로부터 멀리 떨어져 있다는 것을 나타냅니다. 즉 위의 예에서는 귀무가설의 평균을 160이라고 할 수 있어요.

그리고 나서 수집한 표본(예: 학생들의 키)을 사용하여 실제 평균 키가 이 가설을 지지하는지 아니면 반박하는지를 검증합니다.

t-값은 실제 표본 데이터(학생들의 키)의 평균이 160cm와 얼마나 차이가 있는지, 그리고 그 차이가 통계적으로 유의미한지를 판단하는 데 사용됩니다. 표본의 평균 키가 160cm에서 상당히 멀어질수록, 분자가 증가하기 때문에 t-값은 더 크게 나타나게 되고, 이는 귀무가설에 대한 의심을 증가시킵니다. (t 통계량이 커지기 때문에) 반대로, 표본 평균이 160cm에 가깝다면 t-값은 작게 나타나며, 이는 귀무가설을 지지하게 됩니다.

2. 분모의 역할: ( s / \sqrt{n} )

분모는 표본의 표준오차입니다. 표준편차를 표본 크기의 제곱근으로 나누어줌으로써, 우리는 표본 평균의 분산도를 조정합니다. 이는 표본 크기가 클수록 표본 평균이 모집단 평균에 더 가까울 것이라는 통계적 원리를 반영합니다. 즉, 큰 표본 크기는 더 작은 표준오차를 초래하고, 이는 분모를 줄여 t-값을 증가시킵니다.

잘 이해가 안가신다면 아래 문단을 참고하세요.

일표본 t-검정에서의 분모, 즉 표본의 표준오차는 평균 값의 정확도를 나타냅니다. 이걸 이해하기 위해 예를 들어보겠습니다.

상상해 보세요, 여러분이 사탕 가게에서 사탕을 한 움큼 집어서 그 무게를 재본다고 해봅시다. 한 번만 재보는 것과 다섯 번이나 열 번 재보는 것 사이에는 큰 차이가 있겠죠? 여러 번 재보면 재는 값의 평균이 실제 사탕 가게 사탕 무게의 평균에 더 가까울 거라고 믿게 됩니다. 여기서, 여러 번 재보는 행위는 ‘큰 표본 크기’에 해당하고, 그로 인해 우리의 ‘평균’은 더 정확해집니다.

이제, 이를 표준오차에 적용해볼게요:

• 표본의 표준편차(s): 이것은 사탕의 무게가 평균에서 얼마나 멀리 퍼져 있는지를 말합니다. 사탕 무게가 각각 다르기 때문에, 이 편차는 무게의 ‘퍼짐’을 나타냅니다.
• 표본 크기의 제곱근(n에 루트): 이것은 여러분이 사탕을 몇 번이나 재봤는지를 나타냅니다. 재는 횟수가 많을수록, 평균 무게는 실제 더 정확해집니다.
• 표본의 표준오차(s/ n에 루트): 이것은 여러분의 평균 무게 측정값이 얼마나 정확한지, 즉 실제 사탕 무게의 평균과 얼마나 가까운지를 나타냅니다. 여러분이 사탕을 더 많이 재볼수록(즉, 표본 크기가 클수록), 표준오차는 줄어들고, 이는 평균 무게 측정값이 더 정확하다는 것을 의미합니다.

따라서, 표본 크기가 클수록, 즉 더 많이 재볼수록, 표준오차는 작아집니다. 표준오차가 작아지면, t-값의 분모가 작아지므로, t-값은 커지게 됩니다. 그래서, 우리는 더 큰 표본을 사용할 때, 우리의 평균 측정값이 실제로 더 정확하다고 느끼게 됩니다.

3. t-값의 의미

• t-값이 임계치보다 크다는 것은, 기각역에 위치하고 있음을 말하는 동시에 표본 평균과 귀무가설의 평균 사이에 상당한 차이가 있음을 의미합니다. 이 경우, 우리는 귀무가설이 우리 표본 데이터를 잘 설명하지 못한다고 판단할 수 있습니다. 귀무가설을 기각하고 연구가설을 채택합니다.
• t-값이 작다는 것은 표본 평균이 귀무가설의 평균에 가깝다는 것을 의미하며, 이는 귀무가설이 우리 표본 데이터를 비교적 잘 설명할 수 있다는 것을 의미합니다. 귀무가설을 기각하지 않고 연구가설을 채택하지 않습니다.

마지막으로, 이 계산된 t-값은 특정 t 분포(자유도에 따라 달라지는)와 비교되어 p-값을 결정합니다. p-값이 특정 기준(예: 0.05)보다 작으면, 우리는 귀무가설을 기각하고 표본이 우리가 테스트하는 평균값과는 통계적으로 유의미하게 다르다고 결론짓습니다.

단일 모집단 평균차이검증 t-test 검증 방법 자세히 알아보기

한 백화점에서 과거 소비자 불평건수는 일평균 15건 이상이었다. 관리자는 몇개월간 소비자 만족향상을 위해 노력했고 이에 따라 불평 건수가 과거에 비해 줄어들었을 것이라고 예상한다. 최근 29일간의 불평건수를 조사한 결과 평균 13.5건, 표준편차 4건으로 나타났다. 이러한 자료로 볼 때 불평건수가 줄어 들었다고 할 수 있을까?? *유의수준 = 0.05

1. 가설 설정:

• 귀무가설 (H0): 불평 건수는 줄어들지 않았다. 즉, 일평균 불평 건수는 여전히 15건 이상이다. (( \mu = 15, \mu > 15 ))
• 대립가설 (H1): 불평 건수가 줄어들었다. 즉, 일평균 불평 건수는 15건 미만이다. (( \mu < 15 ))

2. 유의 수준 설정:

위에 나온대로 유의 수준(α)은 0.05로 설정합니다. 이는 우리가 귀무가설을 기각하는 데 있어 5%의 오류 확률을 허용한다는 의미입니다.

3. 통계량 계산:

표본 평균은 13.5건, 표본의 표준편차는 4건이고, 표본 크기(n)는 29입니다. 일표본 t-검정 통계량은 다음과 같이 계산됩니다:

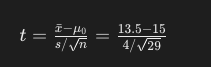
이 값을 계산해 보겠습니다.

계산 결과, t-값은 약 -2.02입니다.

4. 임계값 결정 및 결론 도출 (자유도 계산)

일표본 t-검정에서 유의 수준이 0.05일 때, 자유도(df)는 ( n – 1 = 29 – 1 = 28 )입니다. 일반적인 t 분포 표를 참조하면, 유의 수준 0.05와 자유도 28에 해당하는 단측 검정의 임계값은 약 -1.701 혹은 그보다 더 작은 값(음수 값으로)입니다.

여기서 계산된 t-값은 -2.02이고, 이는 -1.701보다 더 작습니다. 이는 우리의 t-값이 임계 영역 안에 들어간다는 것을 의미합니다. 따라서, 우리는 귀무가설 ( \mu \geq 15 )을 기각할 수 있습니다.

결론:

계산된 t-값과 임계값을 비교한 결과, 유의 수준 0.05에서 귀무가설을 기각합니다. 이는 백화점의 노력이 효과가 있었으며, 불평 건수가 실제로 줄어들었다는 것을 통계적으로 의미합니다. 따라서, 최근 29일간의 데이터를 바탕으로 볼 때, 백화점의 일평균 불평 건수는 과거보다 감소했다고 할 수 있습니다.