카이제곱 적합성 검증 이론, 공식, 검증절차

카이제곱 적합성 검증 이론 정리
귀무가설은 관측된 빈도와 예상빈도의 차이가 없다는 가설 (기대빈도와 같음)
카이제곱 적합성 검증의 자유도는 셀의 수-1이다.

카이제곱 적합성 검증 이론

카이제곱 적합성 검정(Chi-Square Goodness-of-Fit Test)은 관측된 데이터가 특정 이론적 분포나 예상된 비율에 얼마나 잘 맞는지를 통계적으로 검정하는 방법입니다. 이 검정은 주로 하나의 범주형 변수에 대해 사용되며, 그 변수의 여러 카테고리가 특정 비율로 분포되어 있는지를 알아보고자 할 때 사용됩니다.

카이제곱 적합성 검정의 과정:

1. 귀무 가설(H0) 설정: 관측된 빈도가 예상된 빈도와 차이가 없다는 가설을 세웁니다. 즉, 실제 데이터가 이론적 분포나 예상된 비율에 적합하다는 가설입니다.
2. 대립 가설(H1) 설정: 관측된 빈도와 예상된 빈도 사이에는 유의미한 차이가 있다는 가설을 세웁니다. 즉, 실제 데이터가 이론적 분포나 예상된 비율에 적합하지 않다는 가설입니다.
3. 기대 빈도 계산: 각 카테고리에 대한 예상되는(이론적인) 빈도를 계산합니다. 예를 들어, 주사위를 던져서 각 숫자가 나올 예상 빈도는 모든 숫자가 동일한 확률로 나올 것으로 예상됩니다.
4. 카이제곱 통계량 계산: 관측된 빈도와 기대된 빈도 사이의 차이를 이용하여 카이제곱 통계량을 계산합니다. 이 값은 데이터가 이론적 분포에 얼마나 잘 맞는지를 나타내는 지표입니다.
5. 결론 도출: 계산된 카이제곱 통계량을 카이제곱 분포와 비교하여 통계적 유의성을 판단합니다. 만약 계산된 값이 임계값보다 크면 귀무 가설을 기각하고, 데이터가 이론적 분포에 적합하지 않다는 결론을 내립니다.

예시:

주사위를 60번 던져 각 면이 10번씩 나올 것으로 기대하고 있지만, 실제로는 각 면이 나온 횟수가 다릅니다. 카이제곱 적합성 검정을 사용하여, 실제 관측된 빈도가 이 이론적 기대(각 면이 동일한 확률로 나온다는 가정)와 유의미한 차이가 있는지를 검증할 수 있습니다.

간단히 말해서, 카이제곱 적합성 검정은 실제 관측된 데이터가 어떤 이론적 분포나 예상 비율에 얼마나 잘 부합하는지를 검증하는 통계적 방법입니다.

카이제곱 기대빈도 공식

기대 빈도는 각 범주(또는 그룹)에 대해 이론적으로 예상되는 관측치의 수입니다.

카이제곱 통계량 공식

카이제곱 통계량은 관측된 빈도와 기대 빈도 사이의 차이를 정량화하는 데 사용됩니다

문제로 이해하기

한 자동차 제조회사의 신제품개발 담당자는 현재 신제품 승용차의 색깔대안을 다섯가지 고려하고 있으며, 어떤 색을 더 선호하는지 여부를알고자한다. 300명의 소비자들에게 색 대안 ABCDE의 승용차를 보여주고, 가장 선호하는 것을 조사한 결과 표와같이나타났다. 이 자료로부터 각 색깔을 선호하는 소비자들의 비율이 다르다고할 수 있을까? 유의수준(a)=0.05

이 문제를 해결하기 위해 카이제곱 적합성 검정을 사용하여 각 색깔을 선호하는 소비자들의 비율이 모두 같다는 귀무 가설을 검증할 수 있습니다. 제공된 데이터와 유의수준을 바탕으로 검증 과정을 진행하겠습니다.

1. 가설 설정

• 귀무 가설 (H0): 모든 색깔을 선호하는 소비자들의 비율은 같다. (각 색깔에 대한 선호도에 차이가 없다)
• 대립 가설 (H1): 적어도 한 색깔을 선호하는 소비자들의 비율이 다르다. (하나 이상의 색깔에 대한 선호도에 차이가 있다)

제공된 데이터에 따르면, 5가지 색깔에 대한 선호도 조사 결과는 다음과 같습니다:

• A 색깔: 88명
• B 색깔: 65명
• C 색깔: 52명
• D 색깔: 40명
• E 색깔: 55명
• 총: 300명

2. 기대 빈도 계산

귀무 가설 하에서 모든 색깔이 동등하게 선호된다고 가정하면, 각 색깔에 대한 기대 빈도는 300명을 5로 나눈 값, 즉 각 색깔에 대해 60명이 됩니다.

3. 카이제곱 통계량 계산

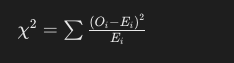
여기서 (O_i)는 각 색깔에 대한 관측된 빈도이고, (E_i)는 기대 빈도(60명)입니다.

이제 Python을 사용하여 카이제곱 통계량을 계산하고, 이 값을 유의수준 0.05에서의 카이제곱 분포 임계값과 비교하여 결론을 도출하겠습니다.

카이제곱 통계량은 관측된 빈도와 기대 빈도 사이의 차이를 기반으로 계산됩니다. 이 경우에, 각 색깔에 대한 기대 빈도는 60명이며, 우리는 다음과 같이 카이제곱 통계량을 계산할 수 있습니다:

여기서 (O_i)는 관측된 빈도이고, (E_i)는 기대 빈도입니다. 각 색깔에 대해 이 계산을 수행한 후, 모든 결과를 더하여 최종 카이제곱 통계량을 얻습니다.

이렇게 계산하면 통계량은 21.63이 나옵니다.

4. 자유도와 유의수준:

이 검정의 자유도는 카테고리의 수에서 1을 뺀 값입니다. 이 경우에는 5가지 색깔이 있으므로 자유도는 4입니다. 유의수준(( a ))은 0.05로 설정되었습니다.

5. 결론 도출:

계산된 카이제곱 통계량을 자유도가 4인 카이제곱 분포의 임계값과 비교합니다. 유의수준 0.05에서 자유도가 4인 카이제곱 분포의 임계값은 대략 9.49입니다. 계산된 통계량이 이 임계값보다 크다면, 귀무 가설을 기각하고 각 색깔을 선호하는 소비자들의 비율이 다르다고 결론지을 수 있습니다.

카이제곱 통계량은 21.63이었으므로 임계값(obs)9.49보다 크므로, 해당 귀무가설은 기각되고, 우리는 각 색깔을 선호하는 소비자들의 비율이 다르다고 결론을 내릴 수 있습니다.