일원분산분석 이론, 공식, 검증 절차 (

Estimated reading: 1 minute 0 views

일원분산 분석 필수 체크포인트
1. 하나의 독립변수, 세 개 이상 집단간의 평균값 차이가 있는지 검사
2. 각 집단간 평균을 낸 후 > 분산분석표를 작성해야 함 (SST와 SSE를 구해야 한다)
3. 이후 작성한 분산분석표를 바탕으로 F 통계량을 도출한다.
4. F 임계치를 바탕으로 귀무가설을 기각할지 결정한다. F crit(a;k-1,n-k) 이때 k는 집단 간 수고 n은 전체 집단 내 요소들의 수이다.

일원분산분석 원리

일원분산분석(ANOVA: Analysis of Variance)은 세 개 이상의 집단 간에 평균값이 차이가 있는지를 검증하는 통계적 방법입니다. 이 방법은 여러 집단 간에 비교를 할 때 주로 사용되며, 특히 각 집단의 데이터가 정규 분포를 이루고 독립적이며, 분산이 동일할 때 유효합니다. 이때 일원이라는 말 처럼, 원인은 하나라는 말입니다. 즉 종속변수에 영향을 주는 원인변수(독립변수)는 하나입니다.

일원분산분석의 기본 원리:

전체 변동(Total Variation): 관측값 전체가 얼마나 퍼져 있는지를 나타냅니다. 이는 각 관측값과 전체 관측값의 평균과의 차이를 제곱하여 합한 것으로 계산됩니다.
집단 내 변동(Within-Group Variation): 각 집단 내에서 관측값이 얼마나 퍼져 있는지 나타냅니다. 각 집단 내의 관측값들이 해당 집단의 평균에서 얼마나 벗어나 있는지를 측정합니다.
집단 간 변동(Between-Group Variation): 각 집단의 평균이 전체 평균에서 얼마나 벗어나 있는지를 측정합니다. 이는 각 집단의 평균이 전체 평균과 얼마나 다른지를 보여줍니다.

일원분산분석의 절차:

가설 설정:

귀무 가설(H0): 모든 집단의 평균이 동일하다.
대립 가설(H1): 적어도 하나의 집단의 평균이 다르다.

분산 분석 표 작성: 데이터를 분석하여 집단 내 변동과 집단 간 변동을 계산하고, 이를 토대로 분산 분석 표를 작성합니다.
F-통계량 계산: 집단 간 변동을 집단 내 변동으로 나누어 F-통계량을 계산합니다. F-통계량은 집단 간 차이가 집단 내 차이에 비해 얼마나 큰지를 나타냅니다.
가설 검정: 계산된 F-통계량과 F-분포를 비교하여 P-값을 얻고, 이를 통해 귀무 가설을 기각할지 여부를 결정합니다. 일반적으로 P-값이 0.05 미만이면 귀무 가설을 기각하고, 적어도 하나의 집단 평균이 다른 것으로 간주합니다.

예시:

세 개의 다이어트 프로그램을 비교하기 위해 각각의 프로그램에 참여한 사람들의 체중 감량 결과를 분석하는 경우, 일원분산분석을 사용하여 세 프로그램의 평균 체중 감량이 서로 다른지 검정할 수 있습니다.

일원분산분석은 여러 집단의 평균값 비교에 유용하며, 분석 결과는 연구자가 집단 간 차이의 존재 여부를 결정하는 데 도움을 줍니다. 다만, 어떤 집단이 다른 집단과 다른지 구체적으로 알아보기 위해서는 사후 검정(Post-hoc tests)이 필요할 수 있습니다.

문제로 이해하기

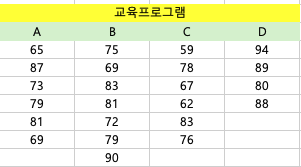
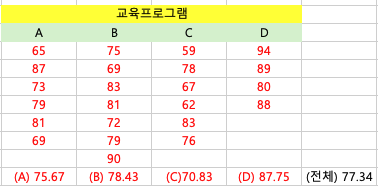
A 잡지회사의 영업부에서는 영업사원 교육을 위해 네 가지 교육프로그램의 효과에 차이가 있는지를 조사하기 위해 실험을 실시했다. 이 실험에서 28명의 신입사원들을 무작위로 네 집단으로 나누어 교육프로그램 ABCD로서 교육을 실시했다. 교육도중 5명이 탈락했고, 교육을 마친 후 1주일간의 판매실적은 표와 같다. 여기서 신입사원들을 무작위로 네 집단으로 나누었고, 각 집단에 속한 사원들의 교육이전 판매능력은 동일하다고 했을 때, 교육프로그램에따라 판매실적이 다르다고할 수 있을까? (유의수준 a=0.05)

이 문제를 해결하기 위해 일원분산분석(ANOVA) 검정 절차를 단계별로 설명하고 계산을 진행하겠습니다.

1. 가설 설정

귀무 가설(H0): 모든 교육 프로그램(A, B, C, D)의 판매 실적 평균이 동일하다.
대립 가설(H1): 적어도 하나의 교육 프로그램의 판매 실적 평균이 다르다.

2. 데이터 정리

교육 프로그램별 판매 실적을 위의 표에서 확인할 수 있습니다. 이 데이터를 사용하여 각 프로그램의 평균, 분산 등을 계산할 것입니다.

3. 분산 분석 (평균값 구하고, SST와 SSE 구하기)

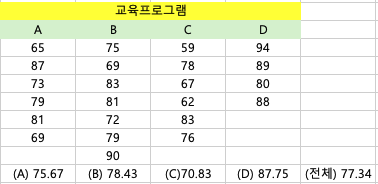
전체 평균(Total Mean), 집단 간 분산(Between-Group Variance), 집단 내 분산(Within-Group Variance)을 계산합니다.
집단 간 분산: 각 집단 평균이 전체 평균과 얼마나 다른지를 나타냅니다.
집단 내 분산: 각 집단 내에서 개별 데이터가 그 집단의 평균과 얼마나 다른지를 나타냅니다.

SST와 SSE 구하기

분산분석표를 제작하기 위해서는 위의 자료 (각 집단의 평균값과 전체 평균값)를 토대로 SST와 SSE를 구해주어야 합니다.
여기서 SST는 집단간 변동성이고 SSE는 집단내 변동성입니다.

집단 간 변동성(SST: Sum of Squares for Treatment)과 집단 내 변동성(SSE: Sum of Squares for Error)을 구하기 위한 계산 과정을 아래에 설명하겠습니다.

SST (집단 간 변동성) 구하기

집단 간 변동성(SST)은 각 집단 평균이 전체 평균과 얼마나 차이가 있는지를 나타냅니다. 계산 공식은 다음과 같습니다.

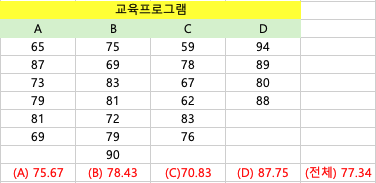
SST=6(75.67-77.34)^2 + 7(78.43-77.34)^2 + ..... + 4(87.75-77.34)^2 = 712.5
집단간 변동성이기 때문에 총 4번을 계산하게 됩니다.

SSE (집단 내 변동성) 구하기

집단 내 변동성(SSE)은 각 집단 내에서 개별 데이터가 해당 데이터가 속한 집단의 평균과 얼마나 차이가 있는지를 나타냅니다. 계산 공식은 다음과 같습니다.

SSE = (65-75.67)^2 + (87-75.67)^2 + .... + (88-87.75)^2 = 1196.63
집단내 변동성이기 때문에 총 23번을 계산해야해요.

계산 결과, 집단 간 변동성(SST: Sum of Squares for Treatment)은 약 712.59이고, 집단 내 변동성(SSE: Sum of Squares for Error)은 약 1196.63입니다.

이는 각 집단의 평균이 전체 평균과 얼마나 차이가 있는지(SST)와 각 집단 내에서 개별 데이터가 해당 집단의 평균과 얼마나 차이가 있는지(SSE)를 나타냅니다. 이러한 값들은 분산분석표에 기록되어, 교육 프로그램 간의 판매 실적 차이가 통계적으로 유의미한지를 평가하는 데 사용됩니다.

4. F-통계량 계산 (분산분석표 제작)

F-통계량은 집단 간 분산을 집단 내 분산으로 나눈 값입니다. 이 값이 크면 클수록 귀무 가설을 기각할 가능성이 높아집니다.
이를 위해서 분산분석표를 제작합니다. 위의SST와 SSE를 바탕으로 분산분석표를 채워줍니다. 분산분석표의 공식은 아래와 같고, 실제 데이터 값으로 채운 것은 그 아래의 사진입니다.

분산분석표

분산분석표는 실험의 결과를 요약하여, 처리(집단 간)와 오차(집단 내)에 대한 정보를 제공합니다. 제시하신 분산분석표를 바탕으로 각 항목을 설명드리겠습니다.

분산분석표 설명

제곱합(SS: Sum of Squares)

처치(집단 간) SS (SST: Sum of Squares for Treatment): 집단 간 변동성을 나타내며, 각 집단 평균이 전체 평균과 얼마나 차이가 있는지를 제곱하여 합한 값입니다. 여기서는 712.5입니다.

오차(집단 내) SS (SSE: Sum of Squares for Error): 집단 내 변동성을 나타내며, 각 데이터가 해당 데이터가 속한 집단의 평균과 얼마나 차이가 있는지를 제곱하여 합한 값입니다. 여기서는 1196.6입니다.

자유도(d.f: degrees of freedom)

처치(집단 간) d.f: 집단 간 변동의 자유도로, 집단의 수에서 1을 뺀 값입니다. 여기서는 집단이 4개이므로 3입니다.

오차(집단 내) d.f: 집단 내 변동의 자유도로, 전체 데이터 수에서 집단의 수를 뺀 값입니다. 여기서는 23개의 데이터에서 4개의 집단을 뺀 19입니다.

평균제곱(MS: Mean Square)

처치(집단 간) MS (MST: Mean Square for Treatment): 집단 간 제곱합을 집단 간 자유도로 나눈 값입니다. 여기서는 237.5입니다.

오차(집단 내) MS (MSE: Mean Square for Error): 집단 내 제곱합을 집단 내 자유도로 나눈 값입니다. 여기서는 63입니다.

F통계량

집단 간 평균제곱을 집단 내 평균제곱으로 나눈 값입니다. 여기서는 3.77입니다. 이 값은 집단 간 변동이 집단 내 변동에 비해 얼마나 큰지를 나타냅니다. F통계량이 더 크면 귀무 가설을 기각할 가능성이 높아집니다.

분산분석표는 실험 결과를 분석하고 해석하는 데 있어 중요한 역할을 합니다. 제시된 분산분석표는 앞서 계산한 결과와 일치하며, F통계량을 바탕으로 한 P-값을 통해 귀무 가설의 기각 여부를 결정할 수 있습니다. 이미 설명드린 바와 같이, P-값이 0.05 이하인 경우 귀무 가설을 기각하고, 적어도 하나의 교육 프로그램이 다른 프로그램들과 비교하여 판매 실적에 유의미한 차이를 만들어낸다고 결론 내릴 수 있습니다.

5. 결론 도출 (임계치 계산)

임계값(F crit)으로 결론 도출하기

계산된 F-통계량을 F-분포 표와 비교하여 P-값을 찾습니다. P-값이 0.05(유의 수준 α) 이하이면 귀무 가설을 기각하고, 적어도 하나의 교육 프로그램의 판매 실적 평균이 다르다고 결론지을 수 있습니다.
F crit(임계치)는 F crit(a;k-1,n-k)로 계산됩니다. 즉 F crit(0.05; 3,19)라서 대략 3.13로 계산됩니다.
통계량은 3.77이고 임계치는 3.13이기 때문에 귀무가설이 기각됩니다.
결론: 네 가지 교육 프로그램 중 하나 이상이 다른 프로그램들과 비교했을 때 판매 실적에 유의미한 차이를 만들어 낸다.

P값으로 결론 도출하기

계산 결과, F-통계량은 약 3.77이며, 해당 F-통계량에 대한 P-값은 약 0.028입니다. 이는 유의 수준 0.05(α = 0.05)보다 작으므로, 귀무 가설을 기각합니다. 즉, 네 가지 교육 프로그램(A, B, C, D) 중 적어도 하나의 프로그램의 판매 실적 평균이 다른 프로그램들과 다르다는 결론을 내릴 수 있습니다.

이 결과는 네 가지 교육 프로그램 중 하나 이상이 다른 프로그램들과 비교했을 때 판매 실적에 유의미한 차이를 만들어낸다는 것을 의미합니다. 따라서, 이러한 차이를 더 구체적으로 분석하기 위해서는 사후 검정(Post-hoc tests)을 수행할 필요가 있습니다.