분산도의 측정: 범위, 분산, 표준편차
분산도의 측정은 데이터가 얼마나 퍼져 있는지, 즉 데이터의 변동성을 나타내는 통계적 수치입니다. 여기에는 범위(range), 분산(variance), 표준편차(standard deviation)가 포함됩니다. 이 측정치들은 모두 데이터 세트 내의 값들이 얼마나 서로 다른지를 나타내는 데 사용됩니다.
범위 (Range)
- 정의: 범위는 데이터 세트에서 가장 큰 값과 가장 작은 값의 차이입니다. 범위는 데이터가 얼마나 넓게 퍼져 있는지를 가장 간단하게 나타내는 측정치입니다.
- 계산: 최대값 – 최소값
- 예시: 학생들의 시험 점수가 60, 70, 80, 90, 100점이라면, 이 데이터 세트의 범위는 100 – 60 = 40점입니다.
- 주의점: 범위는 이상치에 매우 민감하며, 데이터의 전반적인 분포는 고려하지 않습니다.
분산 (Variance)
- 정의: 분산은 각 데이터 값이 평균에서 얼마나 떨어져 있는지를 나타내는 측정치입니다. 즉, 데이터의 퍼짐 정도를 나타냅니다.
- 계산: (각 데이터 값 – 평균)^2의 합을 데이터 개수로 나눈 값 (표본 분산의 경우, 데이터 개수에서 1을 뺀 값으로 나눕니다).
- 예시: 시험 점수의 평균이 80점이고, 점수가 60, 70, 80, 90, 100점인 경우, 각 점수의 평균으로부터의 차이를 제곱하여 더한 후, 이를 점수의 수로 나누어 분산을 계산할 수 있습니다.
- 주의점: 분산은 원래 데이터 값과 단위가 다릅니다(예: 점수의 분산은 ‘점수 제곱’ 단위로 표시됩니다). 따라서 해석하기 어려울 수 있습니다.
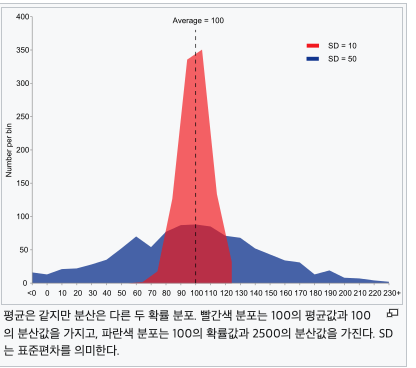
분산이 크면 데이터의 변동성이 크다?
분산이 크다는 것은 데이터의 변동성이 크다는 것을 의미합니다. 즉, 개별 데이터 포인트들이 그들의 평균값으로부터 멀리 떨어져 분포되어 있다는 것을 나타냅니다. 이는 데이터 세트 내의 값들이 서로 상당히 다르다는 것을 의미하며, 평균으로부터의 이러한 큰 차이들은 전반적인 데이터 세트의 분산을 증가시킵니다. 따라서 분산의 크기는 데이터 포인트들이 얼마나 다양하거나 퍼져 있는지를 나타내는 좋은 지표가 됩니다.
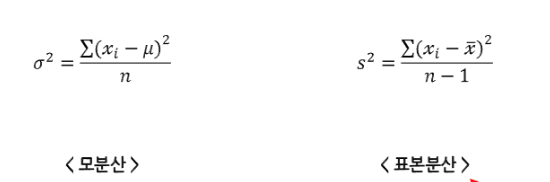


표준편차 (Standard Deviation)

- 정의: 표준편차는 분산의 제곱근으로, 데이터 값들이 평균으로부터 얼마나 떨어져 있는지를 나타내는 측정치입니다. 분산보다 더 일반적으로 사용되며, 데이터의 단위와 동일합니다.
- 계산: 분산의 제곱근 (위의 그림 참고)
- 예시: 위 시험 점수의 분산이 200점^2이라면, 표준편차는 √200 = 약 14.14점입니다.
- 주의점: 표준편차 역시 이상치에 민감하지만, 분산보다 해석하기 쉬운 단위로 표현됩니다.
범위, 분산, 표준편차는 모두 중요한 통계적 측정치이며, 각기 다른 상황에서 유용하게 사용됩니다. 표준편차와 분산은 데이터의 일반적인 변동성을 평가하는 데 주로 사용되며, 범위는 데이터 세트의 전체적인 퍼짐 정도를 빠르게 파악하는 데 사용됩니다.
분산은 데이터의 변동성을 정확하게 계산할 때 사용되며, 주로 이론적이거나 모델링 상황에서 유용합니다.
표준편차는 분산에 기반을 두고 있지만, 실제 데이터의 단위와 일치하여, 일상적인 해석이나 실용적인 상황에서 더 쉽게 사용됩니다.
편차,분산,표준편차,표준오차와의 관계
- 편차(Deviation): 데이터 포인트와 그 데이터 세트의 평균 사이의 차이입니다. 즉, 각 데이터 포인트가 평균으로부터 얼마나 멀리 떨어져 있는지를 나타냅니다. 예를 들어, 데이터 포인트가 평균보다 높다면 편차는 양수가 되고, 평균보다 낮다면 편차는 음수가 됩니다.
- 분산(Variance): 편차의 제곱의 평균입니다. 즉, 각 데이터 포인트가 평균으로부터 얼마나 멀리 떨어져 있는지(편차)의 제곱을 모두 더한 후, 데이터의 총 개수로 나눈 값입니다. 분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 측정하는 지표로, 데이터의 퍼짐 정도를 나타냅니다.
- 표준편차(Standard Deviation): 분산의 제곱근입니다. 표준편차는 분산과 마찬가지로 데이터의 퍼짐 정도를 나타내지만, 편차와 같은 단위로 표현되기 때문에 해석하기 더 쉽습니다. 예를 들어, 편차와 데이터 포인트가 같은 단위(예: 미터, 킬로그램)로 측정된다면, 표준편차도 같은 단위로 표현됩니다.
- 표준오차(Standard Error): 표본 평균의 표준편차입니다. 즉, 여러 번의 표본 추출을 통해 얻은 여러 표본 평균들이 모집단의 실제 평균으로부터 얼마나 떨어져 있는지를 나타내는 지표입니다. 표준오차는 일반적으로 표본의 표준편차를 표본 크기의 제곱근으로 나눈 값으로 계산됩니다. 이는 표본의 크기가 클수록 표본 평균이 모집단 평균에 더 가까울 것이라는 원칙을 반영합니다.
각각의 관계:
- 분산은 편차의 제곱을 이용해 계산됩니다.
- 표준편차는 분산의 제곱근이며, 이는 데이터의 분포 정도를 원래의 단위로 되돌려 해석 가능하게 합니다.
- 표준오차는 표본의 표준편차를 표본 크기의 제곱근으로 나눈 것으로, 표본 평균이 모집단 평균에 얼마나 가까운지를 나타냅니다.
간단히 말해, 편차는 데이터 포인트의 개별적인 퍼짐을 나타내고, 분산은 그 퍼짐의 평균적인 제곱값을, 표준편차는 그 제곱값의 뿌리를 나타내며, 표준오차는 이러한 퍼짐이 평균에 대해 얼마나 잘 추정되는지를 나타냅니다.