중심 경향의 측정: 평균, 중앙값, 최빈값

중심 경향의 측정은 데이터 세트의 중심 또는 평균적인 경향을 파악하기 위한 통계적 수단입니다. 여기에는 평균(mean), 중앙값(median), 최빈값(mode)이 포함됩니다. 이 세 가지 측정치는 모두 데이터 세트의 ‘중심’을 나타내지만, 각기 다른 방식으로 이를 측정합니다.

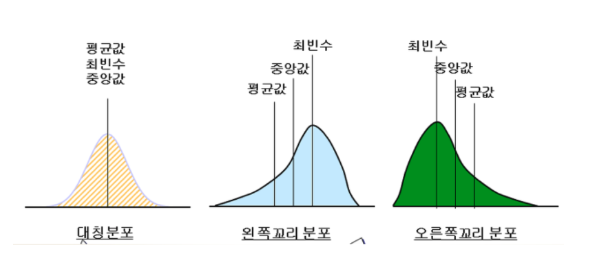
평균 (Mean)

• 정의: 평균은 모든 데이터 값을 합한 후, 데이터의 개수로 나눈 값입니다. 평균은 연속형 데이터에 대한 중심 경향을 측정하는 가장 일반적인 방법입니다.
• 계산: (값1 + 값2 + … + 값n) / n
• 예시: 5명의 학생이 시험에서 받은 점수가 각각 70, 80, 90, 100, 60점이라면, 평균 점수는 (70 + 80 + 90 + 100 + 60) / 5 = 80점입니다.
• 주의점: 평균은 이상치(매우 높거나 낮은 값)에 영향을 받기 쉽습니다. 예를 들어, 한 사람이 매우 높은 소득을 가지고 있다면, 그 집단의 평균 소득은 실제보다 높게 나타날 수 있습니다.

중앙값 (Median)

• 정의: 중앙값은 데이터 세트를 순서대로 나열했을 때 중앙에 위치하는 값입니다. 중앙값은 데이터의 50%가 이 값보다 작고 50%가 이 값보다 큽니다.
• 계산: 데이터를 크기순으로 배열한 후, 가운데 위치하는 값을 찾습니다. 데이터의 개수가 홀수라면, 중앙의 값이 중앙값입니다. 짝수라면, 중앙에 위치한 두 값의 평균이 중앙값이 됩니다.
• 예시: 위와 같은 점수에서 중앙값을 찾기 위해, 점수를 정렬합니다: 60, 70, 80, 90, 100. 여기서 중앙값은 80점입니다.
• 주의점: 중앙값은 이상치의 영향을 덜 받습니다. 따라서 이상치가 많은 데이터 세트에서 중심 경향을 나타내는 데 유용합니다.

최빈값 (Mode)

• 정의: 최빈값은 데이터 세트에서 가장 자주 등장하는 값입니다. 연속형 뿐만 아니라 범주형 데이터에도 사용될 수 있습니다.
• 계산: 데이터 세트에서 가장 많이 나타나는 값입니다.
• 예시: 만약 학생들의 즐겨 입는 색깔이 파랑, 빨강, 파랑, 녹색, 파랑이라면, 최빈색은 ‘파랑’입니다.
• 주의점: 데이터 세트에 가장 빈번한 값이 여러 개 있을 수 있으므로, 최빈값은 한 개 이상일 수 있습니다. 때로는 최빈값이 존재하지 않을 수도 있습니다.

이 세 가지 측정치는 각각 다른 정보를 제공하고, 데이터의 특성에 따라 적합한 중심 경향 측정치가 달라질 수 있습니다. 따라서 분석하고자 하는 데이터의 성질을 고려하여 가장 적합한 측정치를 선택하는 것