척도의 의의와 조건, 필요성, 척도의 유형 (명목,서열,등간,비율)

척도의 의의

척도(scale)는 측정 대상의 특성이나 속성을 정량적으로 표현하기 위해 사용되는 도구 또는 기준입니다. 연구에서 데이터를 수집하고 분석하기 위해 다양한 속성(예: 태도, 선호도, 능력 등)을 숫자나 기호로 변환하는 과정에서 척도가 필요합니다. 척도를 통해 추상적이거나 비가시적인 개념을 구체적이고 측정 가능한 형태로 전환하여, 연구자가 이를 분석하고 해석할 수 있도록 합니다.

척도의 조건 및 필요성

• 정확성(Accuracy): 척도는 측정하고자 하는 속성을 정확하게 반영할 수 있어야 합니다.
• 일관성(Consistency): 동일한 조건에서 반복 측정 시 일관된 결과를 제공해야 합니다.
• 객관성(Objectivity): 측정 결과가 측정자의 주관에 영향을 받지 않아야 합니다.

척도는 연구에서 데이터를 체계적이고 객관적으로 수집, 분석하기 위해 필요합니다. 척도를 사용함으로써 연구 결과의 신뢰성과 타당성을 높이고, 복잡한 현상이나 개념을 이해하고 설명하는 데 도움을 줍니다.

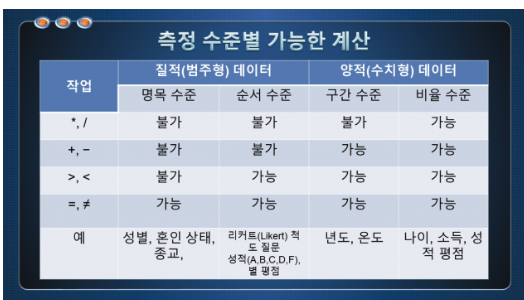
척도의 유형

1. 명목척도 (Nominal Scale):

• 속성이나 특성을 카테고리로 분류하기 위한 척도입니다.
• 숫자는 단순히 레이블로 사용되며, 숫자 간의 수학적 연산은 의미가 없습니다.
• 예: 성별(남성=1, 여성=2), 혈액형(A=1, B=2, AB=3, O=4)

1. 서열척도 (Ordinal Scale):

• 속성이나 특성의 순서나 등급을 나타내는 척도입니다.
• 간격이 일정하지 않아 수학적 연산에 제한이 있습니다.
• 예: 교육 수준(고등학교=1, 대학교=2, 대학원=3), 경기 결과(1등, 2등, 3등)

1. 등간척도 (Interval Scale):

• 속성이나 특성의 간격이 일정한 척도로, 순서와 더불어 간격도 의미를 가집니다.
• 절대 영점이 없어 비율 비교는 불가능합니다.
• 예: 온도 척도(섭씨, 화씨), 지능 지수(IQ)

1. 비율척도 (Ratio Scale):

• 간격이 일정하고 절대 영점을 가진 척도입니다.
• 모든 수학적 연산이 가능하며, 가장 강력한 척도입니다.
• 예: 무게, 키, 시간, 소득

각 척도 유형은 연구의 목적과 대상에 따라 선택되며, 데이터의 측정 및 분석 방법에 영향을 미칩니다. 척도의 선택은 연구 결과의 해석과 유용성에 중요한 역할을 하므로 신중하게 고려되어야 합니다.